Big O Notation Explained Quickly

Big O Notation is a system that measures and compares the performance of code. It introduces specific vocabulary to relay information about how well an algorithm or piece of code is optimized.

This means we need a general language to say how fast a piece of code processes data and how efficiently it allocates and uses memory for its operations. Here we go through what this exactly means.

What is Big O Notation?

To explain, let’s begin with two examples that implement the fibonacci number for a value n in different ways.

function fibLoop(n) {
  let fib = [0, 1];
  for(let i = 2; i < n + 1; i++) {
    fib[i] = fib[i-2] + fib[i-1];
  }
  return fib[n]
}

//fibLoop(30) returns 832040

function fibFormula(n) {
  return Math.round((Math.pow(1.618034, n) - Math.pow((1 - 1.618034), n)) / Math.sqrt(5)) 
}

//fibFormula(30) returns 832040

So they both give the same results. How would you go about analyzing these two algorithms? Which one is better? What does better even mean?

In the context of algorithms, better usually means faster and less memory intensive. That is if you have two programs that output the same result, the one that runs faster and uses less memory is usually better. Pretty straightforward so far.

Time Complexity

How fast is an algorithm relative to the input size.

Let’s measure how fast each of the above algorithms run. For that, we use a method called performance.now() which returns time lapsed in milliseconds.

let t1 = performance.now();
fibLoop(1100)
let t2 = performance.now();
console.log(time: ${t2 - t1} milliseconds)

// returns time: 0.3250000011175871 milliseconds

let t1 = performance.now();
fibFormula(1100)
let t2 = performance.now();
console.log(time: ${t2 - t1} milliseconds)

//returns time: 0.05000000260770321 milliseconds

You can see the second function is clearly faster. But how do you actually quantify that? This is not an exact measurement anyway. Those milliseconds change based on what system you run them on. Or based on how much of the CPU and memory is available to run the task. We need some sort of a system to logically state, in general terms, that the second algorithm is faster than the first.

One way of measuring would be to count the number of operations in each of the algorithms. This way we don’t care what system the algorithms are running on. We also don’t have to wait for an algorithm to finish running. We can just tell which is better by just looking at it.

Now to generalize this idea, we can deduce that all we need is to express a measure of time relative to input size. Put in another way, we describe the relationship between n and how long it takes for an algorithm to finish. This, of course, is related to the number of operations in the algorithm that n affects.

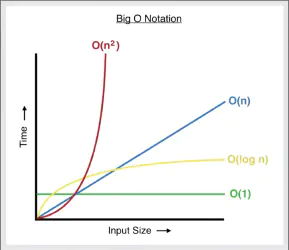
There are a few common scenarios:

1. As n grows, run time doesn’t grow (is constant). i.e. f(n) = 1 (fibFormula)
2. As n grows, run time grows proportionally. i.e. f(n) = n (fibLoop)
3. As n grows, run time grows exponentially. i.e. f(n) = n2

A less common, more complicated scenario: Logarithms. What are they? They are the inverse of exponentiation. If 24= 16 then log is log2(16) = 4. Basically, you’re trying to find the exponent.

4. As n grows, run time grows logarithmically f(n) = log n

Space Complexity

How efficient is an algorithm in using memory relative to its input size.

Space Complexity basically follows the same logic as Time Complexity, except we’re generalizing the space an algorithm takes when n grows. For example, variable assignment is constant (1), but Strings and Arrays are n that is a String of fifty characters takes fifty times more space than a string with 1 character. In our code example, fibLoop space complexity is O(n) whereas fibFormula has a space complexity of O(1)

This is a birds-eye view of what Big O Notation is. If you run into any problems or something is not clear, please drop me a line here. Thanks!